前言
使用有限元方法对三维实体模型进行分析时,同样网格尺寸条件下,相比于四面体单元,六面体单元网格更少、效率和精度更高。
而不管是四面体单元还是六面体单元,都存在一阶和二阶之分,一阶单元精度不如二阶单元,但效率比二阶单元高。
在这篇文章和接下来几篇文章,我会介绍一下一阶六面体单元,即8节点六面体单元的构造及其积分方法,包括:
- 完全积分方法
- 选择减缩积分方法
- 附加9自由度的非协调模式积分方法
- 附加13自由度的非协调模式积分方法
- 减缩积分方法
单元构造
刚度矩阵
三维实体单元的单元刚度矩阵为: \[ \mathbf{k}_e = \int_{V_e}{\mathbf{B}^T \mathbf{DB}} \mathrm{d}V \tag{1} \]
其中,\(\mathbf{D}\) 为弹性矩阵,由材料的弹性模量 \(E\) 和泊松比 \(\nu\) 确定, \[ \mathbf{D} = \frac{E(1 - \nu)}{(1 + \nu)(1 - 2 \nu)} \begin{bmatrix} 1 & \frac{\nu}{1 - \nu} & \frac{\nu}{1 - \nu} & 0 & 0 & 0 \\ \frac{\nu}{1 - \nu} & 1 & \frac{\nu}{1 - \nu} & 0 & 0 & 0 \\ \frac{\nu}{1 - \nu} & \frac{\nu}{1 - \nu} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1 - 2 \nu}{2(1 - \nu)} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1 - 2 \nu}{2(1 - \nu)} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1 - 2 \nu}{2(1 - \nu)} \\ \end{bmatrix} \tag{2} \]
\(\mathbf{B}\) 为应变矩阵, \[ \mathbf{B} = \mathbf{LN} \tag{3} \]
其中,\(\mathbf{L}\) 为微分算子, \[ \mathbf{L} = \begin{bmatrix} \frac{\partial}{\partial x} & 0 & 0 \\ 0 & \frac{\partial}{\partial y} & 0 \\ 0 & 0 & \frac{\partial}{\partial z} \\ \frac{\partial}{\partial y} & \frac{\partial}{\partial x} & 0 \\ 0 & \frac{\partial}{\partial z} & \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} & 0 & \frac{\partial}{\partial x} \end{bmatrix} \tag{4} \]
\(\mathbf{N}\) 为单元形函数。 在实际工程计算中,有限元网格往往是不规则的,直接计算形函数并不方便。 因此,引入自然坐标 \((\xi, \eta, \zeta)\),以简化形函数的计算。 8节点六面体单元在总体(笛卡尔)坐标系与局部(自然)坐标系下的示意图如下所示。
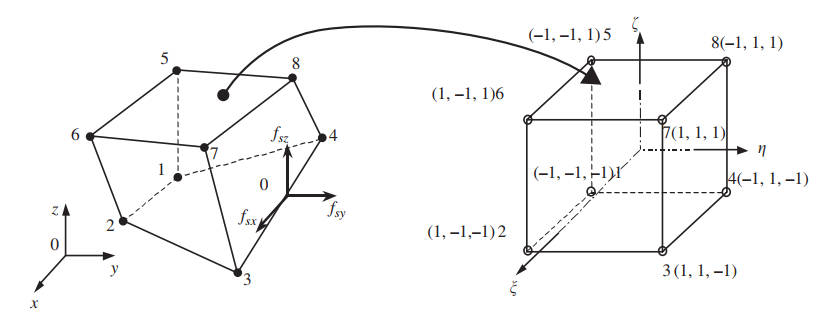
节点按逆时针方向进行编号。
引入自然坐标后,自然坐标系下的形函数为: \[ N_i = \frac{1}{8}(1+\xi \xi_i)(1+\eta \eta_i)(1+\zeta \zeta_i) \tag{5} \]
将其展开,则为: \[ \begin{matrix} N_1 = \frac{1}{8}(1 - \xi)(1 - \eta)(1 - \zeta) \\ N_2 = \frac{1}{8}(1 + \xi)(1 - \eta)(1 - \zeta) \\ N_3 = \frac{1}{8}(1 + \xi)(1 + \eta)(1 - \zeta) \\ N_4 = \frac{1}{8}(1 - \xi)(1 + \eta)(1 - \zeta) \\ N_5 = \frac{1}{8}(1 - \xi)(1 - \eta)(1 + \zeta) \\ N_6 = \frac{1}{8}(1 + \xi)(1 - \eta)(1 + \zeta) \\ N_7 = \frac{1}{8}(1 + \xi)(1 + \eta)(1 + \zeta) \\ N_8 = \frac{1}{8}(1 - \xi)(1 + \eta)(1 + \zeta) \end{matrix} \tag{6} \]
上述形函数定义在自然坐标系 \((\xi, \eta, \zeta)\) 下,而应变矩阵需要的是形函数对总体坐标系 \((x, y, z)\) 求偏导,这就需要用到链式法则: \[ \begin{matrix} \frac{\partial N_i}{\partial \xi} = \frac{\partial N_i}{\partial x} \frac{\partial x}{\partial \xi} + \frac{\partial N_i}{\partial y} \frac{\partial y}{\partial \xi} + \frac{\partial N_i}{\partial z} \frac{\partial z}{\partial \xi}\\ \frac{\partial N_i}{\partial \eta} = \frac{\partial N_i}{\partial x} \frac{\partial x}{\partial \eta} + \frac{\partial N_i}{\partial y} \frac{\partial y}{\partial \eta} + \frac{\partial N_i}{\partial z} \frac{\partial z}{\partial \eta}\\ \frac{\partial N_i}{\partial \zeta} = \frac{\partial N_i}{\partial x} \frac{\partial x}{\partial \zeta} + \frac{\partial N_i}{\partial y} \frac{\partial y}{\partial \zeta} + \frac{\partial N_i}{\partial z} \frac{\partial z}{\partial \zeta} \tag{7} \end{matrix} \]
式(7)可写为矩阵形式: \[ \begin{Bmatrix} \partial N_i / \partial \xi \\ \partial N_i / \partial \eta \\ \partial N_i / \partial \zeta \end{Bmatrix} = \mathbf{J} \begin{Bmatrix} \partial N_i / \partial x \\ \partial N_i / \partial y \\ \partial N_i / \partial z \\ \end{Bmatrix} \tag{8} \] 其中,\(\mathbf{J}\) 称为雅可比矩阵,定义为: \[ \mathbf{J} = \begin{bmatrix} \partial x / \partial \xi & \partial y / \partial \xi & \partial z / \partial \xi \\ \partial x / \partial \eta & \partial y / \partial \eta & \partial z / \partial \eta \\ \partial x / \partial \zeta & \partial y / \partial \zeta & \partial z / \partial \zeta \end{bmatrix} \tag{9} \]
所以,公式(8) 可改写为: \[ \begin{Bmatrix} \partial N_i / \partial x \\ \partial N_i / \partial y \\ \partial N_i / \partial z \\ \end{Bmatrix} = \mathbf{J}^{-1} \begin{Bmatrix} \partial N_i / \partial \xi \\ \partial N_i / \partial \eta \\ \partial N_i / \partial \zeta \end{Bmatrix} \tag{10} \]
公式(10) 可用于计算应变矩阵 \(\mathbf{B}\)。
计算出应变矩阵 \(\mathbf{B}\) 后,公式(1) 可改写为: \[ \mathbf{k}_e = \int_{V_e} \mathbf{B}^T \mathbf{DB} \mathrm{d}V = \int_{-1}^{+1} \int_{-1}^{+1} \int_{-1}^{+1} \mathbf{B}^T \mathbf{DB} \mathrm{det}[\mathbf{J}] \mathrm{d}\xi \mathrm{d}\eta \mathrm{d}\zeta \tag{11} \]
直接计算公式(11)是非常困难的,因此,一般使用数值方法对其进行计算,最常用的是高斯积分方法: \[ \mathbf{I} = \int_{-1}^{+1} \int_{-1}^{+1} \int_{-1}^{+1} f(\xi, \eta, \zeta) \mathrm{d}\xi \mathrm{d}\eta \mathrm{d}\zeta = \sum_{i=1}^n \sum_{i=1}^m \sum_{i=1}^l w_i w_j w_k f(\xi_i, \eta_j, \eta_k) \tag{12} \]
质量矩阵
三维实体单元的质量矩阵为: \[ \mathbf{m}_e = \int_{V_e} \rho \mathbf{N}^T \mathbf{N} \mathrm{d}V \tag{13} \]
可参考式(11),使用形函数进行计算。
载荷列阵
三维实体单元的载荷列阵为: \[ \mathbf{F}_b = \int_{V_e}\mathbf{N}^T \mathbf{f}_b \mathrm{d}V \tag{14} \] 和 \[ \mathbf{F}_s = \int_{S_e}\mathbf{N}^T \mathbf{f}_s \mathrm{d}S \tag{15} \] 其中, \(\mathbf{F}_b\) 和 \(\mathbf{F}_s\) 分别为体力和面力的等效节点载荷。
同样的,可以参考公式(11),使用形函数进行计算。
完全积分
对于8节点六面体单元,如果使用完全积分方法,会产生剪切自锁现象,导致单元刚度增大,结构位移小于理论值。 所以ANSYS和ABAQUS都没有集成完全积分方法(ABAQUS的C3D8单元使用的选择减缩积分方法,我会在下一篇文章中介绍)。
但是,完全积分方法比较基础,从其入门还是很有必要。
一维单元的高斯积分点和权系数如下图所示。
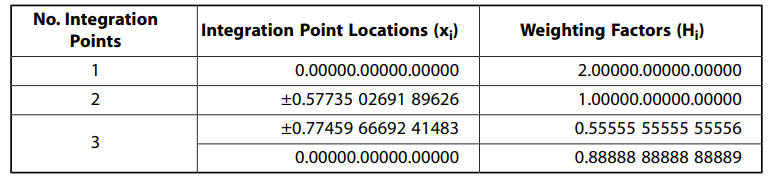
而三维六面体单元的高斯积分点和权系数,可在一维单元高斯积分点和权系数的基础上扩展而来, 即在3个方向上均使用一维的高斯积分点和权系数。
所谓完全积分,指的是在3个方向上,都使用2个积分点进行积分,总共 2x2x2=8个积分点。
以下代码是完全积分方法的核心代码,截取自参考文献[1]:

其中,nip为8,der为形函数对自然坐标的偏导数,jac(前、后)分别为雅可比矩阵和雅可比矩阵的逆,deriv为形函数对总体坐标系的偏导数。截图中使用到的其它子例程,可以下载文献[1]的随书代码进行查看。 需要注意的是,文献[1]中节点编号方式与本文所用的编号方式不同,而本文的节点编号方式是主流方式。
验证
参考文献[1],自编有限元程序。为验证程序的正确性,将其与商业软件进行对比。
由于ANSYS和ABAQUS未集成完全积分方法,因此,使用Nastran进行验证。
Nastran默认也不会使用完全积分方法,需要修改PSOLID卡片,将IN设置为TWO,将ISOP设置为FULL。 1
PSOLID 1 1 TWO FULL
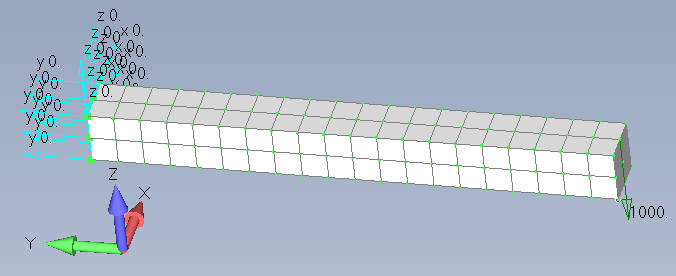
验证模型为长 1000mm 的悬臂梁,梁截面为边长 100mm 的正方形,一端固定,另一端承受 1000N 的集中力。 材料为钢,弹性模量 200000MPa, 泊松比 0.3,如下图所示:
静力学计算结果如下图所示:
可以看出,自编程序的结果(右)在z方向上与Nastran(左)完全一致,x、y方向有细微差别。 这是由于在约束的处理上,自编代码使用了罚函数方法,而Nastran使用了删除行列的方法 (文献[1]也是使用的删除行列的方法,若直接使用文献[1]的代码,其结果将与Nastran完全一致)。
去掉集中力,对模型进行模态分析,分别使用集中质量矩阵和一致质量矩阵,计算结果如下:
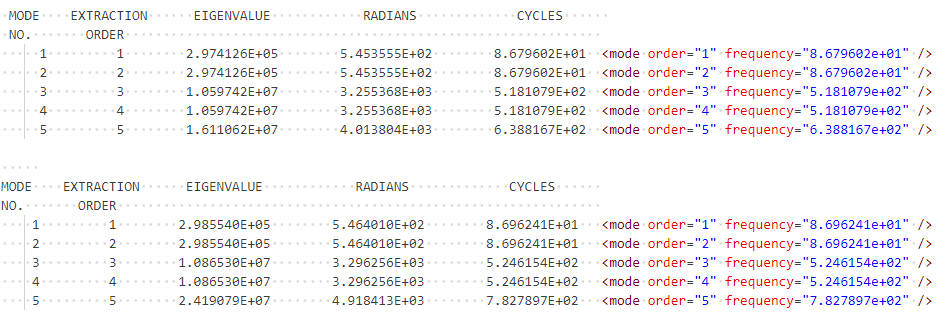
可以看出,无论是集中质量矩阵(上)还是一致质量矩阵(下),自编程序(右)与Nastran(左)计算出的模态频率均一致。
参考文献
[1] Smith I M, Griffiths D V, Margetts L. Programming the finite element method[M]. John Wiley & Sons, 2013.
[2] Liu G R, Quek S S. The finite element method: a practical course[M]. Butterworth-Heinemann, 2013.
[3] 王勖成. 有限单元法[M]. 清华大学出版社有限公司, 2003.
[4] ANSYS Mechanical APDL Theory Reference